Analysis | Graphen von Funktionen

🔎

Verschieben, Strecken und Spiegeln

💡

Der Graph der Funktion $g$ mit $g(x) = a \cdot f(x-c) +d, \ a, c, d \in \R, a \neq 0$ . entsteht aus dem Graphen von $f$ durch:

Verschiebung entlang der x-Achse um $c$

Streckung entlang der y-Achse um den Faktor $a$

Verschiebung entlang der y-Achse um $d$

⚠️

Reihenfolge beachten: „Von innen nach außen denken“. Welche Variablen wirken zuerst auf $x$ ein?

Der Graph der Funktion $g$ entsteht aus dem Graphen von $f$ …

…für $g(x) = -f(x)$ durch Spiegelung an der x-Achse.

…für $g(x) = f(-x)$ durch Spiegelung an der y-Achse.

…für $g(x) = -f(-x)$ durch Spiegelung am Ursprung.

Beispiel

\begin{align*} f(x) &= x^2 \\ g(x) &= 2(x-1)^2 - 3 \end{align*}

Der Graph von $g$ geht aus dem Graphen von $f$ hervor durch:

Verschiebung um $1$ in x-Richtung

Streckung um $2$ in y-Richtung

Verschiebung um $-3$ in y-Richtung

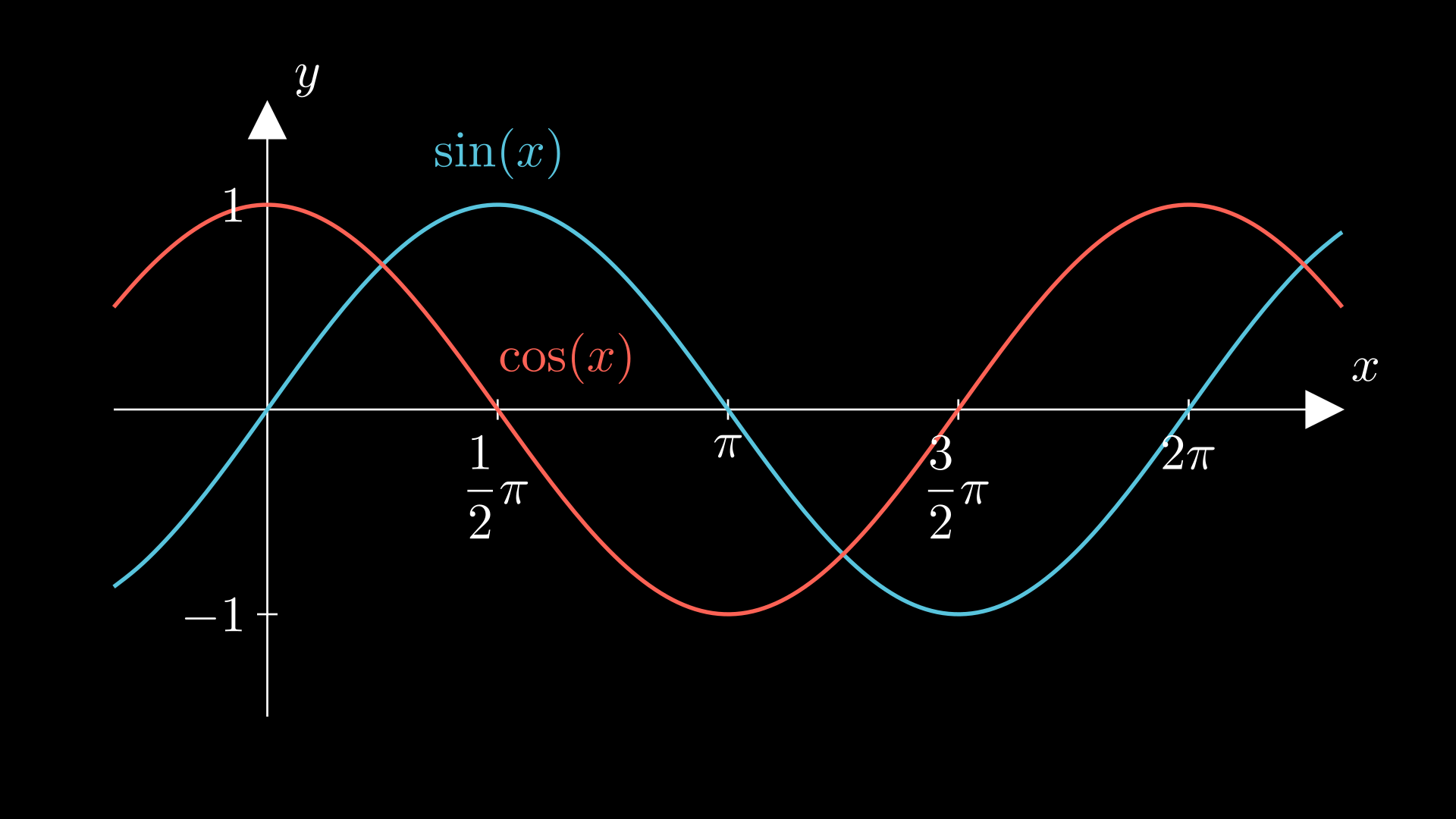
Trigonometrische Funktionen

💡

Der Graph der Funktion $g$ mit $g(x) = a \cdot \sin(b\cdot(x-c))+d, \ a, b, c, d \in \R, a \neq 0, b > 0$ geht aus dem Graphen der Funktion $f$ mit $f(x) = \sin(x)$ hervor durch:

Verschiebung um $c$ in x-Richtung

Stauchung um $b$ in x-Richtung (mit Streckzentrum $(c\ |\ 0)$ )

Streckung um $a$ in y-Richtung

Verschiebung um $d$ in y-Richtung

Die Funktion
$g$ hat die Amplitude $|a|$ und die Periode $\frac{2\pi}b$ .

Beispiel

\begin{align*} f(x) &= \sin(x) \\ g(x) &= 3\cdot\sin(2\cdot(x-1))+4 \end{align*}

Der Graph von $g$ geht aus dem Graphen von $f$ hervor durch:

Verschiebung um $1$ in x-Richtung

Stauchung um $2$ in x-Richtung

Streckung um $3$ in y-Richtung

Verschiebung um $4$ in y-Richtung

Amplitude:
$3$
Periode:
$\frac{2\pi}2 = \pi$

Nullstellen ganzrationaler Funktionen

💡

Satz 1

Sei $f$ eine ganzrationale Funktion vom Grad $n$ und $c$ eine Nullstelle von $f$ . Dann gibt es eine ganzrationale Funktion $g$ vom Grad $n-1$ mit:

f(x) = \underbrace{(x-c)}_{\textsf{Linearfaktor}}\cdot g(x)

Satz 2

Eine ganzrationale Funktion vom Grad $n$ hat höchstens $n$ Nullstellen.

Satz 3

Eine ganzrationale Funktion $f$ , deren Grad ungerade ist, hat mindestens eine Nullstelle

Satz 4

Gegeben sein eine ganzrationale Funktion $f$ mit $f(x) = (x-a)^k \cdot g(x), \ g(a) \neq 0, k \in \N$ .
Dann gilt:

$\pmb{k = 1}:$ Der Graph von $f$ schneidet die x-Achse an der Stelle $a$ . (einfache Nullstelle)

$\pmb{k = 2, 4, 6,…}:$ Der Graph von $f$ hat an der Stelle $a$ einen Extrempunkt auf der x-Achse (zweifache, vierfache usw. Nullstelle)

$\pmb{k = 3, 5, 7,…}:$ Der Graph von $f$ hat an der Stelle $a$ einen Sattelpunkt auf der x-Achse (dreifache, fünffache usw. Nullstelle)

Definition

f(x) = (x-1) \cdot \underbrace{(x-3)^k} _{\textsf{k-fache}\atop \textsf{Nullstelle}}

⚠️

Nicht jede ganzrationale Funktion lässt sich vollständig in Linearfaktoren zerlegen.

Bsp.: $f(x) = x^2 + 1$ , da $f$ keine Nullstellen hat.

Beispiele

$f(x) = (x+2)(x-1)$

$f$ hat bei $x = -2$ und $x = 1$ einfache Nullstellen.

$g(x) = x (x-3)^2$

$g$ hat bei $x=0$ eine einfache Nullstelle und bei $x = 3$ eine Extremstelle

$h(x) = (x+1)^3 (x-1)^2$

$h$ hat bei $x = -1$ einen Sattelpunkt und bei $x = 1$ eine Extremstelle.

Gebrochenrationale Funktionen, Polstellen und senkrechte Asymptoten

💡

Eine Funktion $h$ mit

f(x) = \frac{g(x)}{h(x)}

wobei $g$ und $h$ ganzrationale Funktionen sind, heißt gebrochenrationale Funktion.

💡

Wenn $g(x_0) \neq 0$ und $h(x_0) = 0$ , dann ist $x_0$ eine Polstelle von $f$ und die Gerade mit der Gleichung $x=x_0$ eine senkrechte Asymptote des Graphen von $f$ .

Beispiele

Siehe Beispiele Waagerechte Asymptote.

Waagerechte Asymptote

💡

Sei $f(x) = \frac {g(x)}{h(x)}$ eine gebrochenrationale Funktion mit $a$ und $b$ als Koeffizienten der höchsten Potenzen von $g$ und $h$ , d.h.: $g(x) = a \cdot …, \ h(x) = b \cdot …$ . Dann gilt:

Grad( $g$ ) < Grad( $h$ ): $y = 0$ ist die waagerechte Asymptote der Graphen von $f$

Grad( $g$ ) = Grad( $h$ ): $y = \frac ab$ ist die waagerechte Asymptote der Graphen von $f$

Grad( $g$ ) > Grad( $h$ ): keine waagerechte Asymptote

Zählergrad: Grad( $g$ )
Nennergrad: Grad(
$h$ )

Beispiele

gebrochenrationale Funktion	$f(x) = \frac{4x-1}{3x+3}$	$g(x) = \frac{x^2-1}{x^3-8} + 4$	$h(x) = \frac{x^2-2}{x-1}$	$i(x) = \frac{-x^2+2x-3}{x^2-x-2}$
Polstellen	$x=-1$	$x=2$	$x=1$	$x_1=-1, x_2=2$
senkrechte Asymptoten	$x=-1$	$x=2$	$x=1$	$x = -1$ & $x=2$
waagerechte Asymptote	$y=\frac43$	$y=4$ nicht y = 0 wegen der +4	keine, da Zählergrad > Nennergrad	$y=-1$

Graph eines Funktionsterms

💡

Beim Zusammenhang zwischen Graph und Funktionsterm können folgende Punkte helfen:

Nullstellen und Vielfachheit

Senkrechte Asymptoten und Polstellen

Verhalten für $x \rightarrow \pm\infty$ , ggf. waagerechte Asymptoten

Symmetrie

Extrem- und Wendepunkte

Punktprobe

Beispiele

\begin{align*} f(x) &= x^2 \cdot e^x \\ g(x) &= (x-1)^3 \cdot e^x \\ h(x) &= x^3 - x \\ i(x) &= \frac{x^2}{x^2+1} \end{align*}

Zuordnung:

$f:B ,\ g:C,\ h:D, \ i:A$

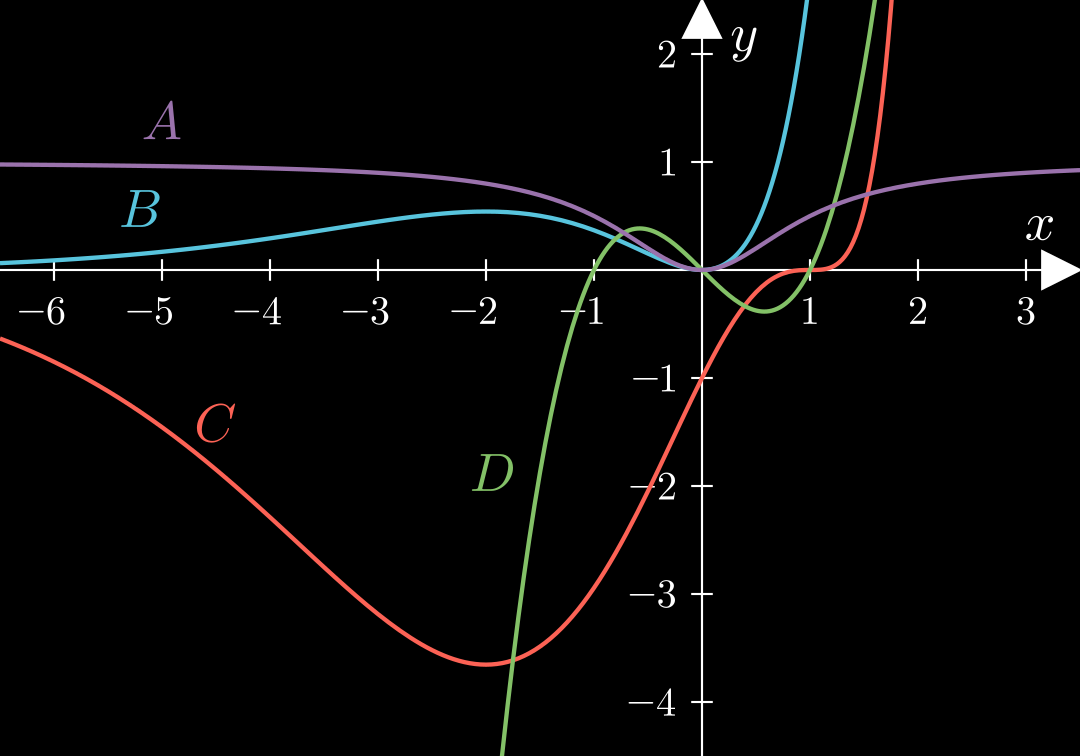
Argumente:

$f:B$

einfache Nullstelle bei $x=0$

Verhalten im Unendlichen:
- $x \rightarrow +\infty: f \rightarrow +\infty$
- $x \rightarrow -\infty: f \rightarrow 0$

$f ≥ 0$

$g:C$

Sattelpunkt bei $x=1$

Verhalten im Unendlichen:
- $x \rightarrow +\infty: f \rightarrow +\infty$
- $x \rightarrow -\infty: f \rightarrow 0$
  - nähert sich $0$ von unten wegen Vorzeichen durch $x^3$

$h:D$

einfache Nullstellen bei $x_0 = -1,\ x_1=0, \ x_2=1$

Verhalten im Unendlichen:
- $x \rightarrow +\infty: f \rightarrow +\infty$
- $x \rightarrow -\infty: f \rightarrow -\infty$

Symmetrisch zum Ursprung

$i : A$

doppelte Nullstelle bei $x=0$

waagerechte Asymptote: $y=1$

Symmetrisch zur y-Achse

⚠️

Es genügen die Argumente, die den Graphen eindeutig von den anderen unterscheiden.

Gemeinsame Punkte einer Funktionsschar

💡

Sei $f_k$ eine Funktionsschar. Um gemeinsame Punkte aller Graphen der Funktionsschar zu bestimmen, genügt es, die Schnittpunkte zweier beliebiger Funktionen der Schar zu finden, da diese Schnittpunkte für alle Graphen gelten müssen. Meist ist die einfachste Gleichung.

f_0(x) = f_1(x)

Beispiel

f_k(x) = (x-1) \cdot e^{-k\cdot x} \\ \begin{align*} \\ f_0(x) &= f_1(x) \\ (x-1)\cdot e^0 &= (x-1)\cdot e^{-x} \\ \Rightarrow x_1=&1 \ \ x_2= 0 \end{align*}

Probe:

\begin{align*} f_k(0) &= (0-1) \cdot e^0 = -1 &\checkmark\ \textsf{unanbähngig von k}\\ f_k(1) &= (1-1) \cdot e^{-k} = 0 &\checkmark\ \textsf{unanbähngig von k} \\ \end{align*} \\ \Rightarrow P(0|-1) \textsf{ und } Q(1|0) \textsf{ liegen auf } \\ \textsf{allen Graphen der Funktionsschar}

❗

Probe machen! Es könnte sein, dass $f_0$ und $f_1$ einen zusätzlichen „zufälligen“ Schnittpunkt haben.

🔎

Zurück zur Übersicht