Stochastik

🔎

Zurück zur Übersicht

Grundbegriffe der Wahrscheinlichkeitsrechnung

Zufallsexperiment

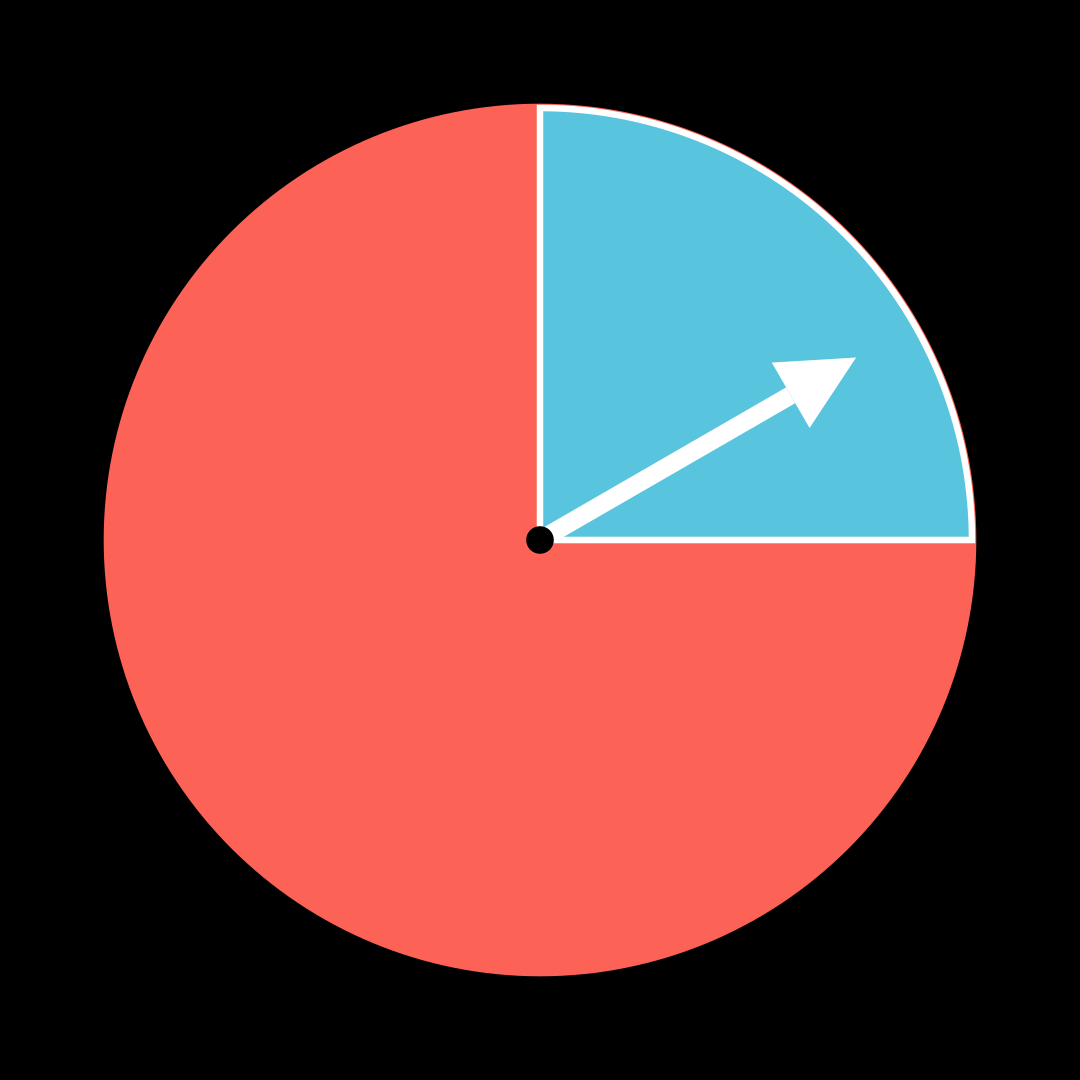
z.B.: „Das Glücksrad wird zweimal Gedreht.“

Ergebnis

z.B.: „zuerst Rot, dann Blau“

Ergebnismenge

S={rr,rb,br,bb}S = \{rr, rb, br, bb\}

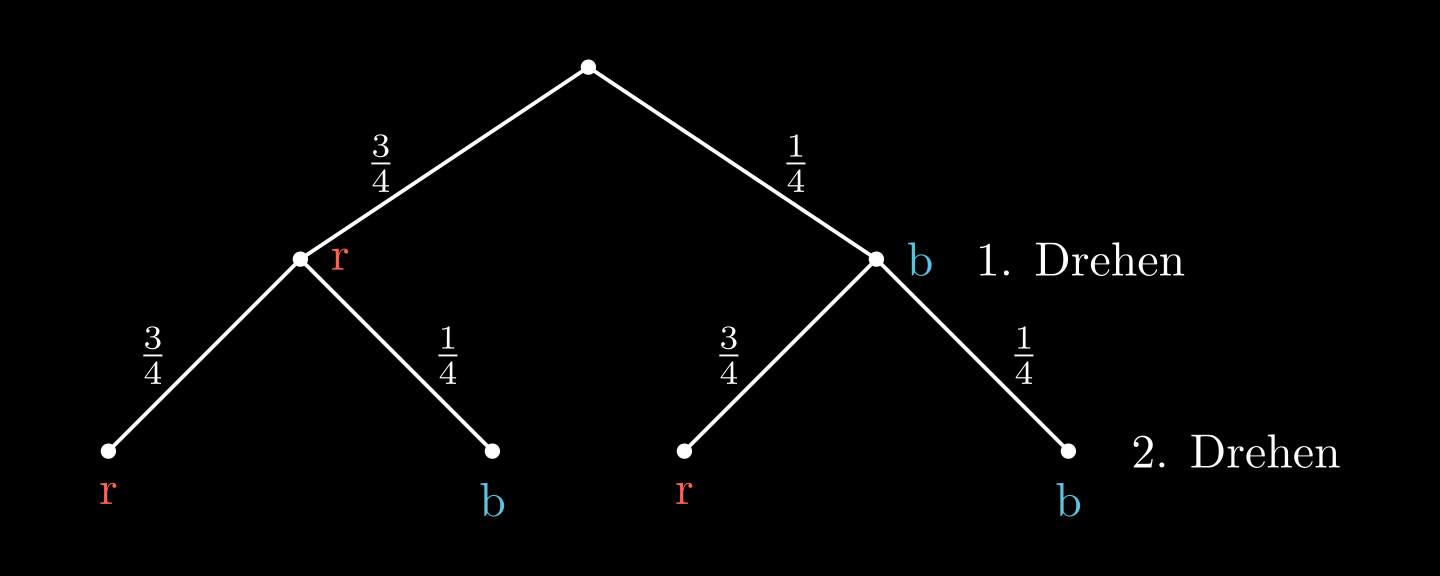
Baumdiagramm

Ereignis

z.B.: „mindestens einmal blau drehen“

Ereignismenge

E={rb,br,bb}E = \{rb, br, bb\}

Gegenereignis

E‾:\overline E{:} „nie blau drehen“ E‾={rr}\quad\overline E = \{rr\}

P(E)=1−P(E‾)=1−P(rr)=1−916=716P(E) = 1 - P(\overline E) = 1-P(rr) = 1- \frac9{16} = \frac7{16}

Produktregel

P(rb)=34⋅14=316P(rb) = \frac34 \cdot \frac14 = \frac3{16}

Summenregel

P(E)=P(rb)+P(br)+P(bb)=716P(E) = P(rb) + P(br) + P(bb) = \frac7{16}

Zufallsvariable

X:X{:} „Gewinn in €“

XXkann die Werte −1,0,4-1, 0, 4 annehmen

Wahrscheinlichkeitsverteilung

Gewinn kk−1-10044
P(X=k)P(X=k)916\frac9{16}716\frac7{16}116\frac1{16}

Erwartungswert von XX

E(X)=−1⋅916+0⋅716+4⋅116=−516⇒ ≈−0,31€E(X) = -1\cdot \frac9{16} + 0 \cdot \frac7{16} + 4 \cdot \frac1{16} = -\frac5{16} \quad\Rightarrow \ \approx-0{,}31€

Varianz

Var(X)=(−1−(−516))2⋅916+(0−(−516))2⋅716+(4−(−516))2⋅116≈1,465(€2)\text{Var}(X) = (-1-(-\frac5{16}))^2 \cdot\frac9{16} +(0-(-\frac5{16}))^2 \cdot\frac7{16} +(4-(-\frac5{16}))^2 \cdot\frac1{16} \approx 1{,}465(€^{\color{red} 2})

Standardabweichung

σ=Var(X)≈1,465=1,21(€)\sigma = \sqrt{\text{Var}(X)} \approx \sqrt{1{,}465} = 1{,}21(€)

Ziehen mit Zurücklegen

💡

Werden aus einer Urne mit nn verschiedene Kugeln, kk Stück herausgezogen, nach jedem Zug wieder zurückgelegt und in ihrer Reihenfolge notiert, so kann die Anzahl an verschiedenen Reihenfolgen berechnet werden mit:

nkn^k

Beispiel

Ein Würfel mit 66 Seiten wird 22 mal gewürfelt. Wie viele mögliche Zahlenpaare gibt es?

Lösung:

62=366^2 = 36

⇒ Es gibt insgesamt 3636 verschiedene Zahlenpaare.

Ziehen ohne Zurücklegen

💡

Werden aus einer Urne mit nn verschiedenen Kugeln, kk Stück nacheinander herausgezogen ohne diese zurückzulegen und in ihrer Reihenfolge notiert, so kann die Anzahl an verschiedenen Reihenfolgen berechnet werden mit:

n!(n−k)!\frac{n!}{(n-k)!}

Beispiel

Ein Wettrennen hat 8 Teilnehmer. Für die schnellsten 33 gibt es Preise. Wie viele Möglichkeiten gibt es, die Preise zu vergeben?

Lösung:

8!(8−3)!=8!5!=8⋅7⋅6⋅5⋅4⋅3⋅2⋅15⋅4⋅3⋅2⋅1=8⋅7⋅6=336\frac{8!}{(8-3)!}=\frac{8!}{5!}= \frac {8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1} {5\cdot4\cdot3\cdot2\cdot1} =8\cdot7\cdot6=336

⇒ Es gibt 336336 verschieden Möglichkeiten die Preise zu vergeben

Ziehen mit einem Griff

💡

Werden aus einer Urne mit nn verschiedenen Kugeln, kk Stück mit einem Griff (gleichzeitig) herausgezogen, so kann man die Anzahl verschiedener Möglichkeiten berechnet werden mit:

(nk)=n!(n−k)!⋅k!\binom nk = \frac{n!}{(n-k)!\cdot k!}

Taschenrechner: n nCr kn \text{ nCr } k

Spezialfälle

(n0)=(nn)=1\binom n0 = \binom nn = 1
(n1)=(nn−1)=n\binom n1 = \binom n{n-1} = n

Beispiel

Ein Verein hat 1010 Mitglieder. Eine Mannschaft besteht aus 44 Spielern. Wie viele mögliche Mannschaften hat der Verein?

Lösung:

(104)=10!(10−4)!⋅4!=10⋅9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅16⋅5⋅4⋅3⋅2⋅1⋅4⋅3⋅2⋅1=10⋅9⋅8⋅74⋅3⋅2⋅1=210\binom{10}{4} = \frac{10!}{(10-4)!\cdot4!} =\frac{ 10\cdot9\cdot8\cdot7\cdot\cancel{6\cdot5\cdot4\cdot3\cdot2\cdot1}}{\cancel{6\cdot5\cdot4\cdot3\cdot2\cdot1}\cdot4\cdot3\cdot2\cdot1} = \frac{10\cdot9\cdot8\cdot7}{4\cdot3\cdot2\cdot1} = 210

⇒ Der Verein hat 210210 mögliche Mannschaften

💬

Ein Trick zum berechnen per Hand ist es, die kk größten Zahlen aus n!n! miteinander zu multiplizieren und durch k!k! zu teilen.
In dem Beispiel oben kommt man dadurch schnell auf den letzten Term mit je
44 Faktoren im Zähler und Nenner. Diese kann man dann oft noch weiter kürzen.

Erwartungswert, Varianz und Standardabweichung

💡

Für eine Zufallsvariable XX, die die Werte x1,x2,...,xnx_1, x_2,..., x_n annehmen kann, definiert man den Erwartungswert μ\mu von XX als:

E(X)=∑i=1nxi⋅P(X=x1)E(X) = \sum_{i=1}^n x_i \cdot P(X=x_1)

E(X)E(X) gibt an, welcher Wert für XX im Durchschnitt auf lange Sicht zu erwarten ist.

Ein Spiel heißt fair, wenn der Gewinn = 0 ist.

💡

Die Varianz

Var(X)=∑i=1n(xi−E(X))2⋅P(X=xi)\text{Var}(X) = \sum_{i=1}^n (x_i-E(X))^2 \cdot P(X=x_i)

und die Standardabweichung

σ=Var(X)\sigma = \sqrt{\text{Var}(X)}

sind Maße für die durchschnittliche Abweichung von XX zum Erwartungswert.

Beispiel

siehe Grundbegriffe der Wahrscheinlichkeitsrechnung

Bedingte Wahrscheinlichkeit

💡

Für zwei Ereignisse AA und BB mit P(A)≠0P(A) \neq 0 ist die bedingte Wahrscheinlichkeit, die Wahrscheinlichkeit für das Eintreten von BB unter der Bedingung, dass AA schon eingetreten ist.

PA(B)=P(A∩B)P(A)P_A(B) = \frac{P(A \cap B)}{P(A)}

Beispiel

U: „Einkauf ist unter 10€.“ K: „Einkauf wird mit Karte bezahlt.“

P(U)=0,4P(U∩K)=0,3PU(K)=P(U∩K)P(U)=0,30,4=0,75⇒Es werden 75% der Einka¨ufe unter 10€ mit Karte bezahlt.P(U) = 0{,}4 \quad P(U \cap K) = 0{,}3 \\ \begin{align*} \\ P_U(K) &= \frac{P(U \cap K)}{P(U)} = \frac{0{,}3}{0{,}4} = 0{,}75 \\ {} \end{align*} \\ \Rightarrow \textsf{Es werden 75\% der Einkäufe unter 10€ mit Karte bezahlt.}

Stochastische Unabhängigkeit

Definition

💡

Zwei Ereignisse AA und BB heißen stochastisch unabhängig, wenn:

P(A∩B)=P(A)⋅P(B)P(A \cap B) = P(A) \cdot P(B)

Satz

💡

Zwei Ereignisse AA und BB sind genau dann stochastisch unabhängig, wenn:

PA(B)=P(B)P_A(B) = P(B)

Denn:

PA(B)=P(A∩B)P(A)=P(A)⋅P(B)P(A)=P(B)P_A(B) = \frac{P(A \cap B)}{P(A)} = \frac{\cancel{P(A)} \cdot P(B)}{\cancel{P(A)}} = P(B)

Beispiel

In einem Betrieb hat 570 Mitarbeiter. Davon fahren 23\frac 23 mit einem Pkw zur Arbeit. Von den 190 auswärtigen Mitarbeitern kommen 177 mit einem Pkw. Untersuche
F: „Fährt mit einem Pkw“ und A: „Kommt von Auswärts“
auf stochastische Unabhängigkeit.

P(F)=23P(A)=190570=13P(F∩A)=177570≈0,311P(F)⋅P(A)=29≠P(F∩A)⇒F und A sind stochastisch abha¨nigig\begin{align*} P(F) &= \frac 23 \\ P(A) &= \frac{190}{570} = \frac 13 \\ P(F \cap A) &= \frac{177}{570} \approx 0{,}311 \\ {} \end{align*} \\ P(F) \cdot P(A) = \frac 29 \neq P(F \cap A) \\ \Rightarrow F \textsf{ und } A \textsf{ sind stochastisch abhänigig}

Bernoulli-Experiment und Bernoulli-Kette

💡

Ein Zufallsversuch mit genau zwei möglichen Ergebnissen heißt Bernoulli-Experiment.

Wenn man ein Bernoulli-Experiment nn-mal wiederholt, sodass die Durchführungen voneinander unabhängig sind, so spricht man von einer Bernoulli-Kette der Länge nn.

Beispiel

5-mal eine Münze werfen ist eine Bernoulli-Kette der Länge 5, da es genau zwei Ergebnisse gibt (Kopf oder Zahl) und ein einzelner Münzwurf keinen Einfluss auf die anderen Münzwürfe hat.

Die Formel von Bernoulli

💡

Für eine Bernoulli-Kette der Länge nn und Trefferwahrscheinlichkeit pp gilt für die Anzahl an Treffern kk:

Ppk(X=k)=(nk)⋅pk⋅(1−p)n−kP_p^k(X=k) = \binom nk \cdot p^k \cdot (1-p)^{n-k}

Man schreibt auch Bn;p(k)B_{n;p}(k) und sagt XX ist binomialverteilt.

💡

Für den Erwartungswert E(X)E(X) gilt:

E(X)=μ=n⋅pE(X) = \mu = n \cdot p

Beispiel

10-facher Münzwurf

n=10p=12X: „Anzahl Zahl (binomialverteilt)“n = 10 \quad p = \frac12 \quad X\text{: „Anzahl Zahl (binomialverteilt)“}

genau 5 mal Zahl

P1210(X=5)⏟WTR: binomialpdf=(105)⋅(12)5⋅(12)10−5≈0,246\underbrace{ P_{\frac12}^{10}(X=5)} _{\textsf{WTR: binomialpdf}} = \binom{10}5 \cdot \left(\frac12\right)^5 \cdot \left(\frac12\right)^{10-5} \approx 0{,}246

höchstens 5 mal Zahl

P1210(X≤5)⏞WTR: binomialcdf=P1210(X=0)+P1210(X=1)+P1210(X=2)+P1210(X=3)+P1210(X=4)+P1210(X=5)=∑k=05P1210(X=k)≈0,623\begin{align*} \overbrace{ P_{\frac12}^{10}(X \leq 5)} ^{\textsf{WTR: binomialcdf}} &= P_{\frac12}^{10}(X = 0) + P_{\frac12}^{10}(X = 1) + P_{\frac12}^{10}(X = 2) \\ &+ P_{\frac12}^{10}(X = 3) + P_{\frac12}^{10}(X = 4) + P_{\frac12}^{10}(X = 5) \\ &= \sum_{k=0}^5 P_{\frac12}^{10}(X = k) \approx 0{,}623 \end{align*}

Umformungen

Ppn(X≥a)=1−Ppn(X≤a−1)Ppn(b≤X≤c)=Ppn(X≤c)−Ppn(X≤b−1)\begin{align*} P_p^n(X \geq a) &= 1-P_p^n(X \leq a-1) \\ P_p^n(b \leq X \leq c) &= P_p^n(X \leq c) - P_p^n(X \leq b-1) \end{align*}

Standardabweichung einer Binomialverteilung

💡

XX ist eine binomialverteilte Zufallsgröße.

σ=n⋅p⋅(1−p)Var(X)=n⋅p⋅(1−p)\begin{align*} \sigma &= \sqrt{n \cdot p \cdot (1-p)} \\ \text{Var}(X) &= n \cdot p \cdot (1-p) \end{align*}

Beispiel

n=10p=0,4σ=10⋅0,4⋅0,6≈1,55n = 10 \quad p = 0{,}4 \\ \sigma = \sqrt{10 \cdot 0{,}4 \cdot 0{,}6} \approx 1{,}55

Zweiseitiger Hypothesentest

Beispiel

💡

Es soll eine Münze überprüft werden:

Nullhypothese H0:p=12H_0: p = \frac12 (Münze ist in Ordnung)

Gegenhypothese (Alternative) H1:p≠12H_1: p \neq \frac12 (Münze ist verbogen)

Signifikanzniveau (maximale Irrtumswahrscheinlichkeit) α^=5%\hat\alpha = 5\%

Gesuchte Grenzen g1g_1 und g2g_2:

P(x≤g1)≤α^2=2,5%P(x≥g2)≥α^2=2,5%P(x \leq g_1) \leq \frac{\hat\alpha}2 = 2{,}5\% \\ P(x \geq g_2) \geq \frac{\hat\alpha}2 = 2{,}5\%

g1g_1 soll dabei möglichst groß und g2g_2 möglichst klein sein.

n=50;X: Anzahl Kopf (binomialverteilt)n = 50; X{:} \text{ Anzahl Kopf (binomialverteilt)}

Tabellenkalkulation

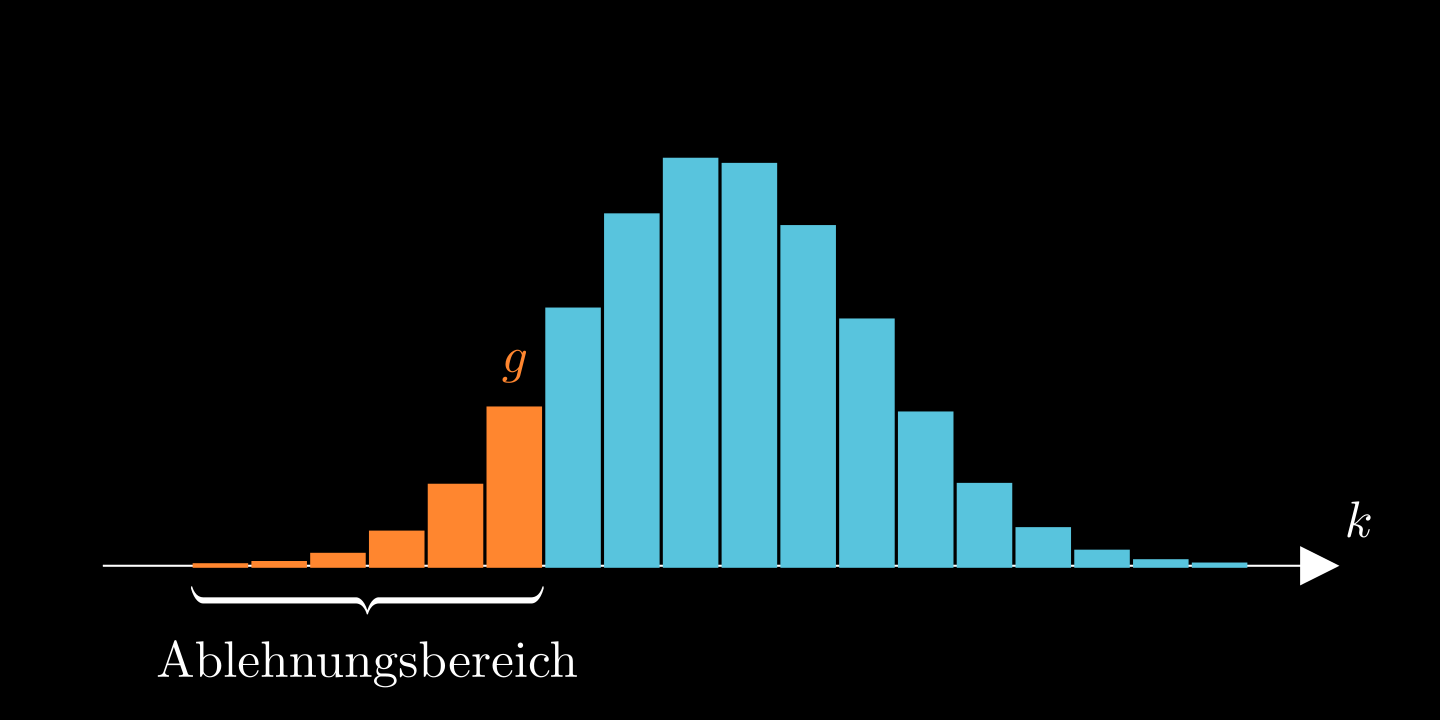
Linksseitiger Test:

g1g_1 ist die größtmögliche Zahl mit P(X≤g1)≤2,5%P(X \leq g_1) \leq 2{,}5\%.

g1g_1P1250(X≤g1)P^{50}_\frac12(X \leq g_1)
17\mathbf{17}0,016\mathbf{0{,}016}kleiner als 2,5%\mathbf{2{,}5\%}
18180,0320{,}032größer als 2,5%2{,}5\%

⇒ g1=17g_1 = 17

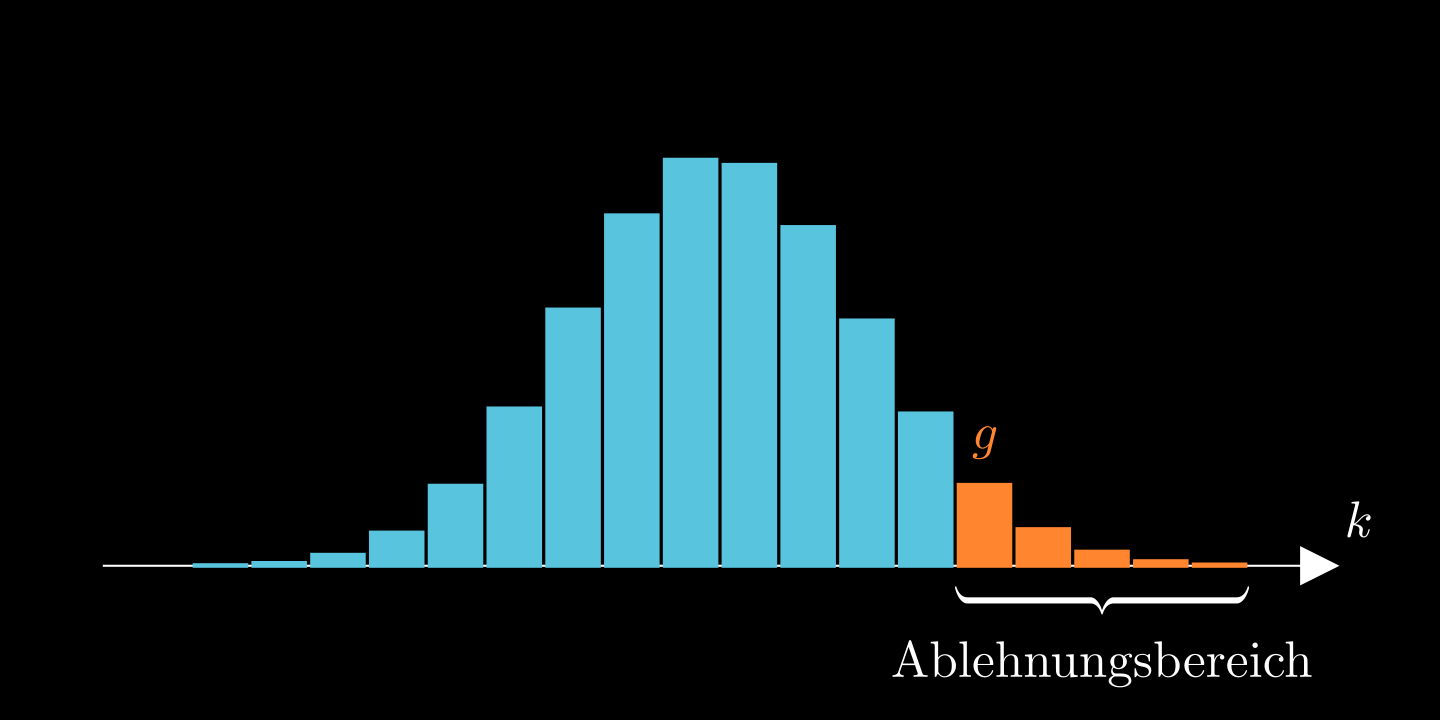
Rechtsseitiger Test:

g2g_2 ist die kleinstmöglichste Zahl mit P(X≥g2)≤2,5%P(X \geq g_2) \leq 2{,}5\%
bzw. die kleinstmöglichste Zahl mit
P(X≤g2−1)≥97,5%P(X \leq g_2-1) \geq 97{,}5\%

g2−1g_2 \color{red} - 1P1250(X≤g2−1)P^{50}_\frac12(X \color{red} \leq\color{default} g_2 \color{red} - 1\color{default})
31310,9680{,}968kleiner als 97,5%97{,}5\%
32\mathbf{32}0,984\mathbf{0{,}984}größer als 97,5%\mathbf{97{,}5\%}

⇒ g2=32+1=33g_2 = 32 \color{red} + 1\color{default} = 33

💡

Ablehnungsbereich der Nullhypothese: {0; 1; …; 17} und {33; …; 50}
Die Nullhypothese wird verworfen, wenn maximal 17 oder mindestens 33 mal Kopf geworfen wird (Münze ist verbogen).

Annahmebereich der Nullhypothese: {18; …; 32}
Die Nullhypothese wird angenommen, wenn mindestens 18 und höchstens 32 mal Kopf geworfen wird (Münze ist in Ordnung).

Irrtumswahrscheinlichkeit:

Die Wahrscheinlichkeit, dass die man denkt, dass die Münze verbogen ist, obwohl sie in Ordnung ist. Sie beträgt:

α=P1250(X≤17⏟g1)+P1250(X≥33⏟g2)≈3,3%≤α^\alpha = P^{50}_\frac12(X \leq \underbrace{17}_{g_1}) + P^{50}_\frac12(X \geq \underbrace{33}_{g_2}) \approx 3{,}3\% \leq \hat\alpha

Einseitiger Hypothesentest

Stichprobenumfang nn und Signifikanzniveau α^\hat\alpha werden festgelegt.

Linksseitiger Test

Nullhypothese: H0:p≥p0H_0: p \geq p_0

Gegenhypothese: H1:p<p0H_1: p < p_0

Ablehnungsbereich: A={0,1,..,g}A=\{0, 1, .., g\}, wobei gg die größte Natürliche Zahl mit

Pp0n(X≤g)≤α^P^n_{p_0}(X \leq g) \leq \hat\alpha
ist.

Rechtsseitiger Test

Nullhypothese: H0:p≤p0H_0: p \leq p_0

Gegenhypothese: H1:p>p0H_1: p > p_0

Ablehnungsbereich: A={g,g+1,…,n}A = \{g, g+1, …, n\}, wobei gg die kleinste natürliche Zahl mit

Pp0n(X≥g)=1−Pp0n(X≤g−1)≤α^P^n_{p_0}(X \geq g) = 1-P^n_{p_0}(X \leq g-1) \leq \hat\alpha
ist.

💡

Man führt eine Stichprobe vom Umfang nn durch.

Entscheidungsregel:

Wenn das Stichprobenergebnis im Ablehnungsbereich liegt, wird H0H_0 verworfen. Ansonsten wird H0H_0 angenommen.

Fehler 1. und 2. Art

💡
H0H_0 ist wahrH0H_0 ist falsch
H0H_0 wird verworfenFehler 1. Art✓\checkmark
H0H_0 wird nicht verworfen✓\checkmarkFehler 2.Art
  • Die Wahrscheinlichkeit für den Fehler 1. Art ist die Irrtumswahrscheinlichkeit α\alpha
  • Die Wahrscheinlichkeit für den Fehler 2. Art ist β\beta und lässt sich nur berechnen, wenn die echte Trefferwahrscheinlichkeit gegeben ist
  • Wenn man nn vergrößert und α^\hat\alpha beibehält, so wird β\beta kleiner
  • Wenn man nn beibehält und α^\hat\alpha verkleinert, so wird β\beta größer
  • α\alpha kann verkleinert werden, indem man α^\hat\alpha verkleinert
  • β\beta kann verkleinert werden, indem man nn vergrößert

In anderen Worten:
Der Fehler 1. Art ist, wenn man im Ablehnungsbereich landet, obwohl die Nullhypothese wahr ist.
Der Fehler 2. Art ist, wenn man nicht im Ablehnungsbereich landet, obwohl die Nullhypothese falsch ist.

Beispiel

Angenommen, eine Firma testet, ob eine neue Batterie eine durchschnittliche Laufzeit von mindestens 10 Stunden hat.

H0H_0: Die Batterie hält weniger als 10 Stunden.

H1H_1: Die Batterie hält mindestens 10 Stunden.

Fehler 1. Art

Der Test ergibt, dass die Laufzeit mindestens 10 Stunden beträgt (H0H_0 wird verworfen), obwohl sie in Wirklichkeit weniger als 10 Stunden beträgt (H0H_0 ist wahr).
→ Die Firma akzeptiert schlechte Batterien.

Fehler 2.Art

Der Test ergibt, dass die Laufzeit weniger als 10 Stunden beträgt (H0H_0 wird angenommen), obwohl sie in Wirklichkeit mindestens 10 Stunden beträgt (H0H_0 ist falsch).
→ Die Firma wirft gute Batterien weg.

Berechnen von α\mathbf{\alpha} und β\mathbf{\beta}

n=50α^=5%H0=p≥0,6H1=p<0,6P0,650(X≤g)≤5%⇒g=23Um β zu berechnen brauchen wir die tatsa¨chlicheWahrscheinlichkeit. Ich gebe sie hier als p=0,55 vor.α=P0,650(X≤23)≈0,0314β=P0,5550(X>23)=1−P0,5550(X≤23)≈0,872n = 50 \quad \hat\alpha = 5\% \\ H_0 = p \geq 0{,}6 \quad H_1 = p < 0{,}6 \\ {}\\ P^{50}_{0{,}6}(X \leq g) \leq 5\% \\ \Rightarrow g = 23 \\{}\\ \textsf{Um β zu berechnen brauchen wir die tatsächliche}\\ \textsf{Wahrscheinlichkeit. Ich gebe sie hier als } p = 0{,}55 \textsf{ vor.} \\{}\\ \begin{align*} \alpha &= P^{50}_{0{,}6}(X \leq 23) \approx 0{,}0314 \\ \beta &= P^{50}_{\color{red}0{,}55} (X {\color{red}>}23) = 1 - P^{50}_{0{,}55}(X \leq 23) \approx 0{,}872 \end{align*}

Wahl der Nullhypothese

💡

Bei einem Hypothesentest wird der Fehler, dass die Nullhypothese H0H_0 aufgrund des Stichprobenergebnisses fälschlicherweise verworfen wird, kontrolliert

Seine Wahrscheinlichkeit ist stets höchstens so groß wie das Signifikanzniveau α^\hat\alpha.

1. Faustregel

Man wählt die Nullhypothese so, dass der Fehler 1. Art derjenige ist, den man vermeiden möchte.

2. Faustregel

Man wählt die Behauptung, die statistisch gestützt werden soll, als Alternative.

Beispiel

Eine Zeitung behauptet, dass sich maximal 85% der Autofahrer angurten. Ein Autoclub bezweifelt dies.

Aus der 2. Faustregel folgt:
Der Autoclub möchte zeigen, dass sich mehr als 85% angurten. Daher wählt man
H1:p>0,85H_1: p > 0{,}85. Daraus folgt H0:p≤0,85H_0: p \leq 0{,}85.

Dadurch ist die 1. Faustregel auch erfüllt:

  • Der Fehler 1. Art ist, dass sich in Wahrheit weniger als 85% angurten, der Autoclub allerdings denkt, dass es mehr als 85% sind.
  • Der Fehler 2. Art ist, dass sich in Wahrheit mehr als 85% angurten, der Autoclub allerdings denkt, dass es weniger als 85% sind.

Der schlimmere Fehler ist der 1. Art, da der Autoclub der Zeitung vorwirft falsche Informationen zu verbreiten. Beim Fehler 2. Art würde im schlimmsten Fall unnötigerweise eine Kampagne zur Förderung des Anschnallens gestartet werden.

💬

Die 1. Faustregel folgt meist aus der 2. Faustregel. Daher ist es oft am einfachsten, nach der 2. Faustregel zu handeln, da diese auch einfacher ist und man nicht argumentieren muss, welcher Fehler schlimmer ist.

Normalverteilung und Gaußsche Glockenfunktion

💡

Eine Zufallsgröße XX heißt normalverteilt mit den Parametern μ\mu (Erwartungswert) und σ\sigma (Standardabweichung), wenn für zwei reellen Zahlen aa und bb mit a≤ba \leq b gilt:
Die Wahrscheinlichkeit, dass
XX Werte zwischen aa und bb annimmt, ist

P(a≤X≤b)=∫abφμ;σ(x) dxP(a \leq X \leq b) = \int_a^b \varphi_{\mu;\sigma}(x) \, dx

Man sagt kurz: XX ist Nμ;σN_{\mu;\sigma}-verteilt. Die Normalverteilung ist eine stetige Verteilung.

💡

Man nennt die Funktion φμ;σ\varphi_{\mu;\sigma} mit

φμ;σ(x)=1σ2π⋅e−(x−μ)22σ2\varphi_{\mu;\sigma}(x) = \frac{1}{\sigma\sqrt{2\pi}} \cdot e^{-\frac{(x-\mu)^2}{2\sigma^2}}

Gaußsche Glockenfunktion und ihren Graphen Gaußsche Glockenkurve.

💡

φμ;σ\varphi_{\mu;\sigma} hat die Extremstelle μ\mu und die Wendestellen μ±σ\mu \pm \sigma und ist die Dichtefunktion einer Nμ;σN_{\mu;\sigma}-verteilten Zufallsgröße.

💡

Es gilt

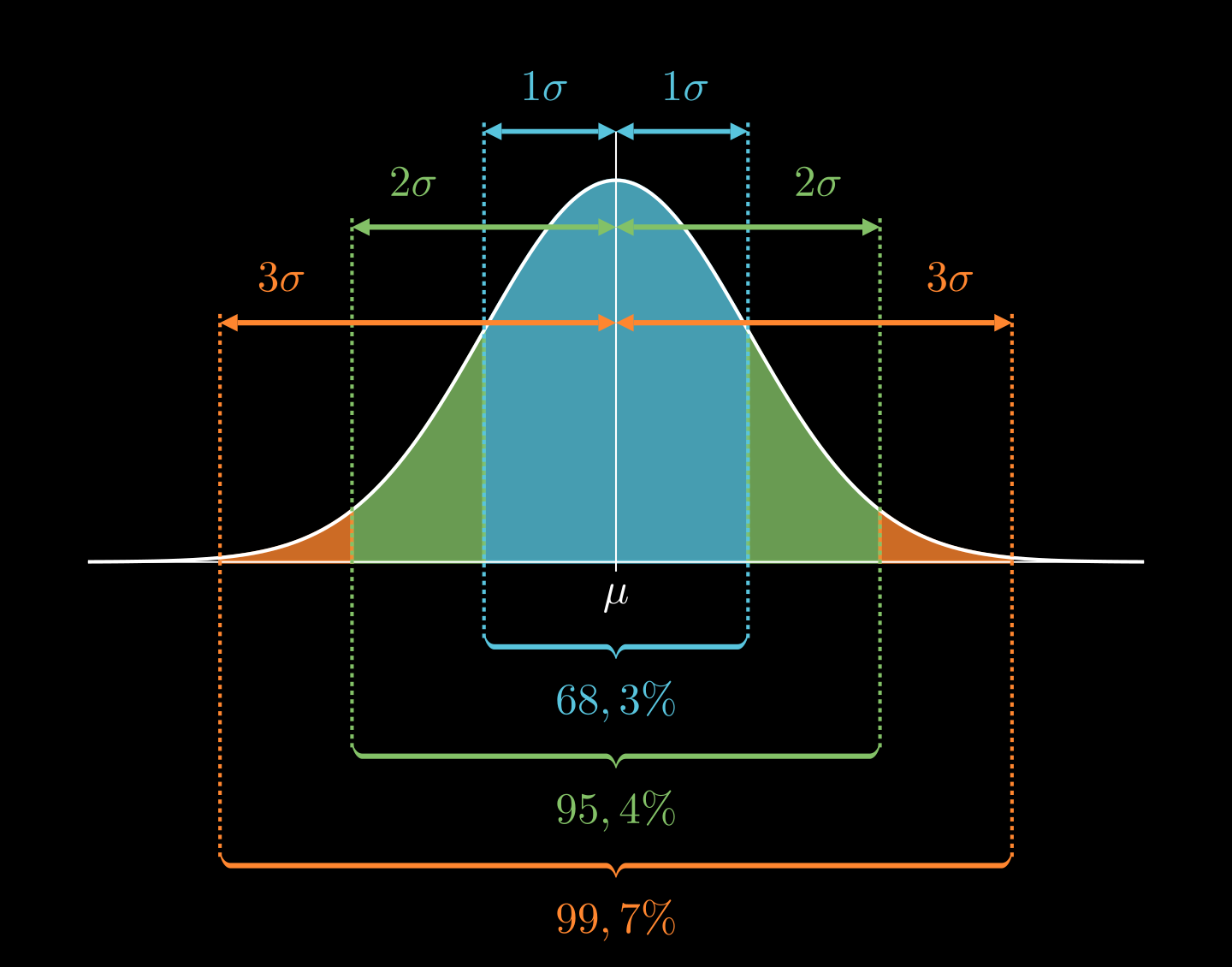
P(X=a)=∫aaφμ;σ(x) dx=0somit gilt auchP(X≤a)=P(X<a)P(X = a) = \int_a^a \varphi_{\mu;\sigma}(x) \, dx =0 \\ \textsf{somit gilt auch} \\ P(X \leq a) = P(X < a)

Zusätzlich gilt:

φμ;σ(x)>0 fu¨r alle x∈R\varphi_{\mu;\sigma}(x) > 0 \text{ für alle } x \in \R
∫−∞+∞φμ;σ(x) dx=1\int_{-\infty}^{+\infty} \varphi_{\mu;\sigma}(x) \, dx = 1

Beispiele

μ=100σ=15P(70≤X<110)=∫70110φ100;15 dx≈0,725P(X<85)=∫−∞85φ100;15 dx≈0,159\mu = 100 \quad \sigma = 15 \\ \begin{align*} P(70 \leq X < 110) &= \int_{70}^{110} \varphi_{100;15} \, dx \approx 0{,}725 \\ P(X < 85) &= \int_{-\infty}^{85} \varphi_{100;15} \, dx \approx 0{,}159 \end{align*}

μ\mu und σ\sigma aus gegebenen Daten ermitteln

💡

Gemessene Daten können häufig durch eine Normalverteilung mit Mittelwert μ\mu und Standardabweichung σ\sigma modelliert werden.
Für die Messwerte
x1,x2,…,xnx_1, x_2, …, x_n gilt:

μ=1n∑i=1nxiσ=1n∑i=1n(xi−μ)2\begin{align*} \mu &= \frac1n \sum_{i=1}^{n}x_i \end{align*} \qquad \begin{align*} \sigma &= \sqrt{ \frac1n \sum_{i=1}^{n}(x_i-\mu)^2 } \end{align*}

Beispiel

Punkte in der nächsten Mathe Klausur:

Messwerte:111315121412
μ=16⋅(11+13+...+12)=16⋅77≈12,83\begin{align*} \mu &= \frac16\cdot(11+13+...+12) \\ &=\frac16\cdot77 \\ &\approx 12{,}83 \end{align*}
σ=16⋅((11−12,83)2+(13−12,83)2...+(12−12,83)2)=16⋅10,83≈1,34\begin{align*} \sigma &= \sqrt{\frac16 \cdot ((11-12{,}83)^2+(13-12{,}83)^2...+(12-12{,}83)^2) } \\ &= \sqrt{\frac16\cdot10{,}83} \\ &\approx 1{,}34 \end{align*}

⇒ Die Messwerte können durch eine N12,83;1,34N_{12,83;1,34}-verteilte Zufallsgröße modelliert werden.

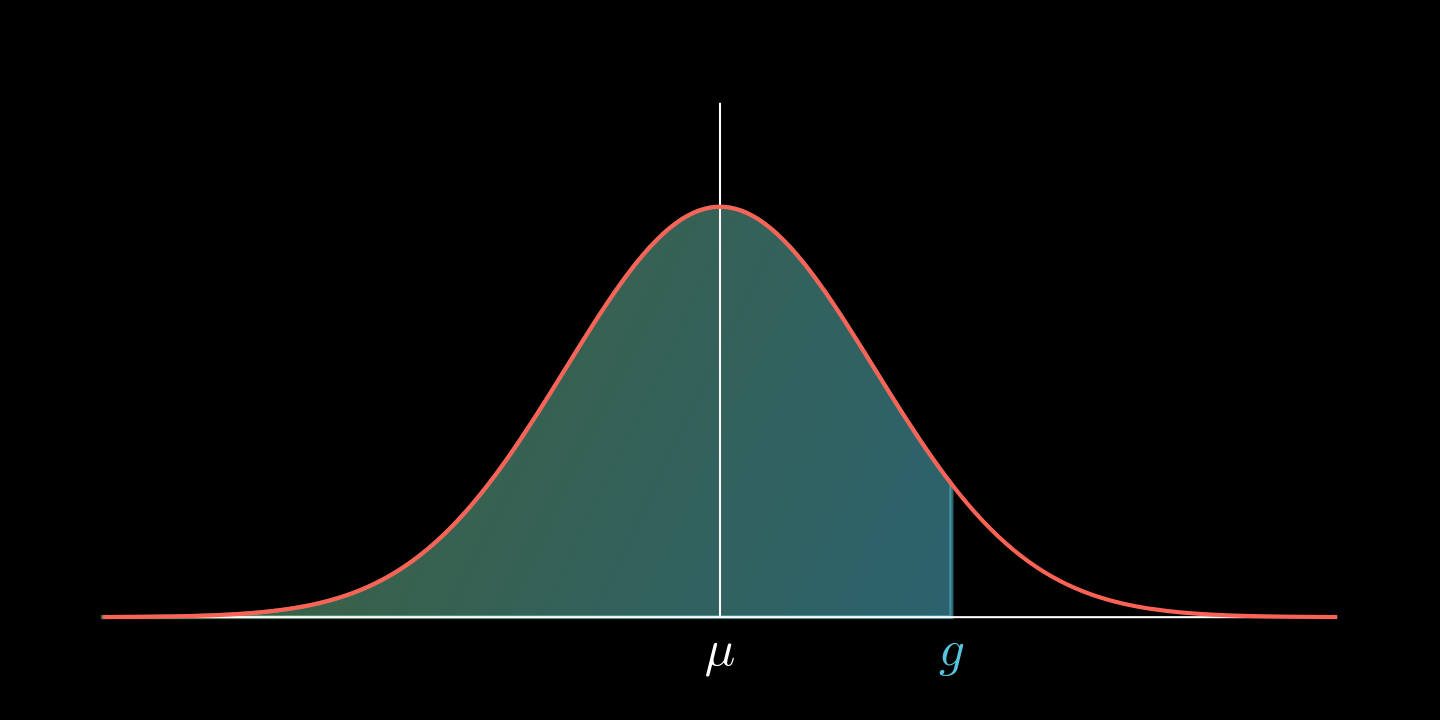
Umkehrung der Normalverteilung

💡

Für eine Nμ;σN_{\mu;\sigma}-verteilte Zufallsgröße XX lässt sich für eine vorgegebene Wahrscheinlichkeit pp durch den WTR-Befehl invNormal die Zahl gg mit P(X≤g)=pP(X \leq g) = p bestimmen.

Beispiel

μ=250σ=20p=0.7invNormal ⇒g≈260,49\mu = 250 \quad \sigma = 20 \quad p = 0.7 \\ \text{invNormal } \Rightarrow g \approx 260{,}49

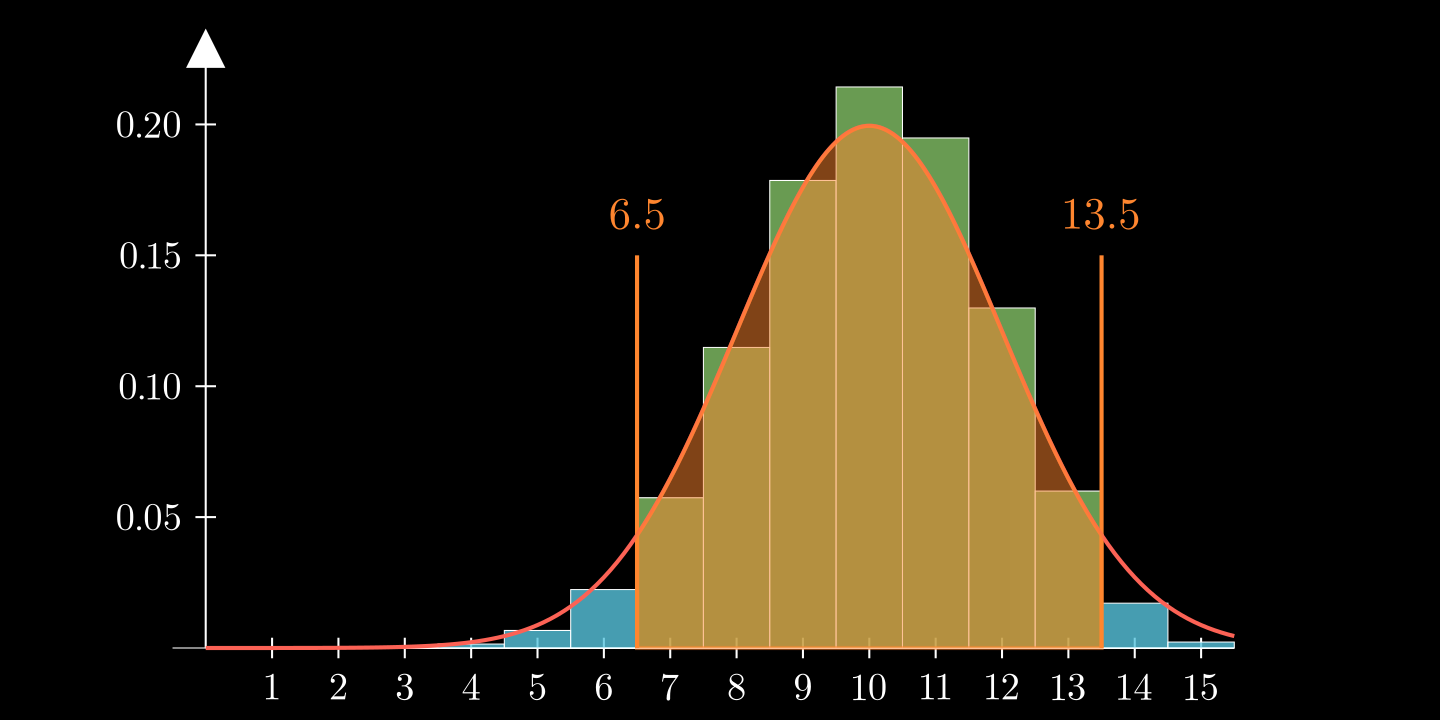
Normalverteilung zur Annäherung einer diskreten Zufallsgröße

💡

Nutzt man die Normalverteilung um die Wahrscheinlichkeit für eine diskrete Zufallsgröße näherungsweise zu bestimmen, muss man die Integralgrenzen entsprechend anpassen.

Beispiel

Notenpunkte 0..150..15 sind N10;2N_{10;2}-verteilt.

P(7≤X≤13)⏟7,8,9,10,11,12,13⏟7 diskrete Werte=∫6,513,5⏟Interval-la¨nge 7φ10;2(x) dx≈0,92\underbrace{P(7 \leq X \leq 13)} _{\underbrace{ 7,8,9,10,11,12,13} _{7 \textsf{ diskrete Werte}}} = \underbrace{ \int_{6{,}5}^{13{,}5}} _{\text{Interval-}\atop \text{länge } 7} \varphi_{10;2}(x) \, dx \approx 0{,}92

Sigma-Regeln

💡

Für eine Nμ;σN_{\mu;\sigma}-verteilte Zufallsgröße gelten folgende Sigma-Regeln

Intervall IIP(X∈I)P(X \in I)
[μ−σ;μ+σ][\mu - \sigma; \mu + \sigma]≈0,683\approx 0{,}683
[μ−2σ;μ+2σ][\mu - 2\sigma; \mu + 2\sigma]≈0,954\approx 0{,}954
[μ−3σ;μ+3σ][\mu - 3\sigma; \mu + 3\sigma]≈0,997\approx 0{,}997

Diese Regeln gelten auch näherungsweise für eine Binomialverteilung.

🔎

Zurück zur Übersicht